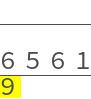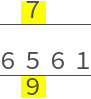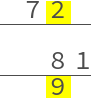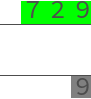
六千五百六十一、九人分之、問人得幾何。
答曰、七百二十九。 |
Six thousand five hundred [and] sixty-one:
[with] nine people sharing it,
[we] ask, how much getteth [each] person?
Answer saith: seven hundred [and] twenty-nine. |
-
In modern notation:
6561 \div 9 = 729.
|
| 術曰、先置六千五百六十一於中位為實、下列九人為法。 |
Method saith:
first put six thousand five hundred [and] sixty-one
upon [the] middle places as [the] dividend,
[and] below [it] rank [the] nine people as [the] divisor. |
|
| 上位置七百、以上七呼下九、七九六十三、即除中位六千三百。 |
[In the] upper places put seven hundred,
[and] calling [the] lower nine with [the] upper seven:
seven nines [are] sixty-three,
that is, remove from [the] middle places six thousand three hundred. |
|
| 退下位一等、即上位置二十、以上二呼下九、二九十八、即除中位一百八十。 |
Retreat [the] lower place [by] one rank,
that is, [in the] upper places put twenty,
[and] calling [the] lower nine with [the] upper two:
two nines [are] eighteen,
that is, remove from [the] middle places one hundred [and] eighty. |
|
| 又更退下位一等、即上位更置九、即以上九呼下九、九九八十一、即除中位八十一。 |
And retreat further [the] lower place [by] one rank,
that is, [in the] upper places put further [a] nine,
that is, call [the] lower nine with [the] upper nine:
nine nines [are] eighty-one,
that is, remove from [the] middle places eighty-one. |
|
| 中位並盡、收下位。上位所得、即人之所得。 |
[The] middle places altogether exhausted, take back [the] lower place.
That which resulteth [in the] upper places, is that gotten of [each] person. |
|
| 自八八六十四至一一如一、並準此。 |
From eight eights [are] sixty-four unto one one [is] as one:
together [be they] standardised [to] this. |
|