-
重: layered
重、平聲、 Cantonese: chʻung4, Mandarin: chóng
- Version B has 頭位 for 上位, both here and in many of the sections to follow.
-
After putting the numbers into two separate rows,
the text tells us to "step" (i.e. shift to the left) the lower number
until its units digit is vertically in line
with the top number's most significant digit.
For example, if we wish to compute 1989 × 64:
Or, in Arabic numerals for readability:
-
命: name
Or maybe "command/order" as in "operate on".
- 過: carried; lit. passed
下位乘訖者、則俱退之。
Those lower places which [be] finished multiplying: retreat them all.
-
訖: finished
訖、居迄切、 Cantonese: kat7, Mandarin: qì
-
A concrete example of the algorithm does not appear until §13,
so I will provide my own.
Here is an animation (crappy source code here)
showing the multiplication 1989 × 64 = 127296,
where I have used usual numerals rather than rods (for readability)
and I have split the middle row into two rows
to make the intermediate additions clearer.
I have greyed out the finished digits instead of removing them:
The algorithm pretty much works like modern long multiplication, except that you go from left to right. Indeed the advantage of using counting rods is that carrying simply consists of putting more rods down, whereas with pen & paper, you must work from right to left and finish all the carrying before proceding to the next digit.
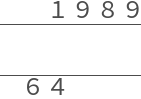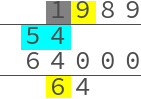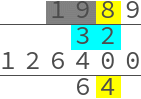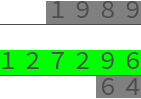
- The instruction 俱退之, "retreat them all", refers to the shifting to the right of the lower number 64, after both the 6 and the 4 have been multiplied through.
-
六不積: sixes not accumulated
This is saying that the digit 6 in rod numerals is displayed either as
or as
, but not as
nor as
.
-
五不隻: fives not single
This is saying that the digit 5 in rod numerals is displayed either as
or as
, but not as
nor as
, since the last two would be indistinguishable from the rod numeral representation for the digit 1.
- Version C erroneously has 土下 for 上下.